Des fleurs pour Schrödinger
Hommage à Laurent Nottale
Contexte
Site de l’exposition :
https://openagenda.com/agendas/62529616/events/40200210
Du 9 mars 2024 au 24 mai 2024 au Conservatoire de Pantin.
Paramètres
- a : échelle
- b : angle
- c : modulation
- d : incurvation
- k : nombre de pétales
Résumé
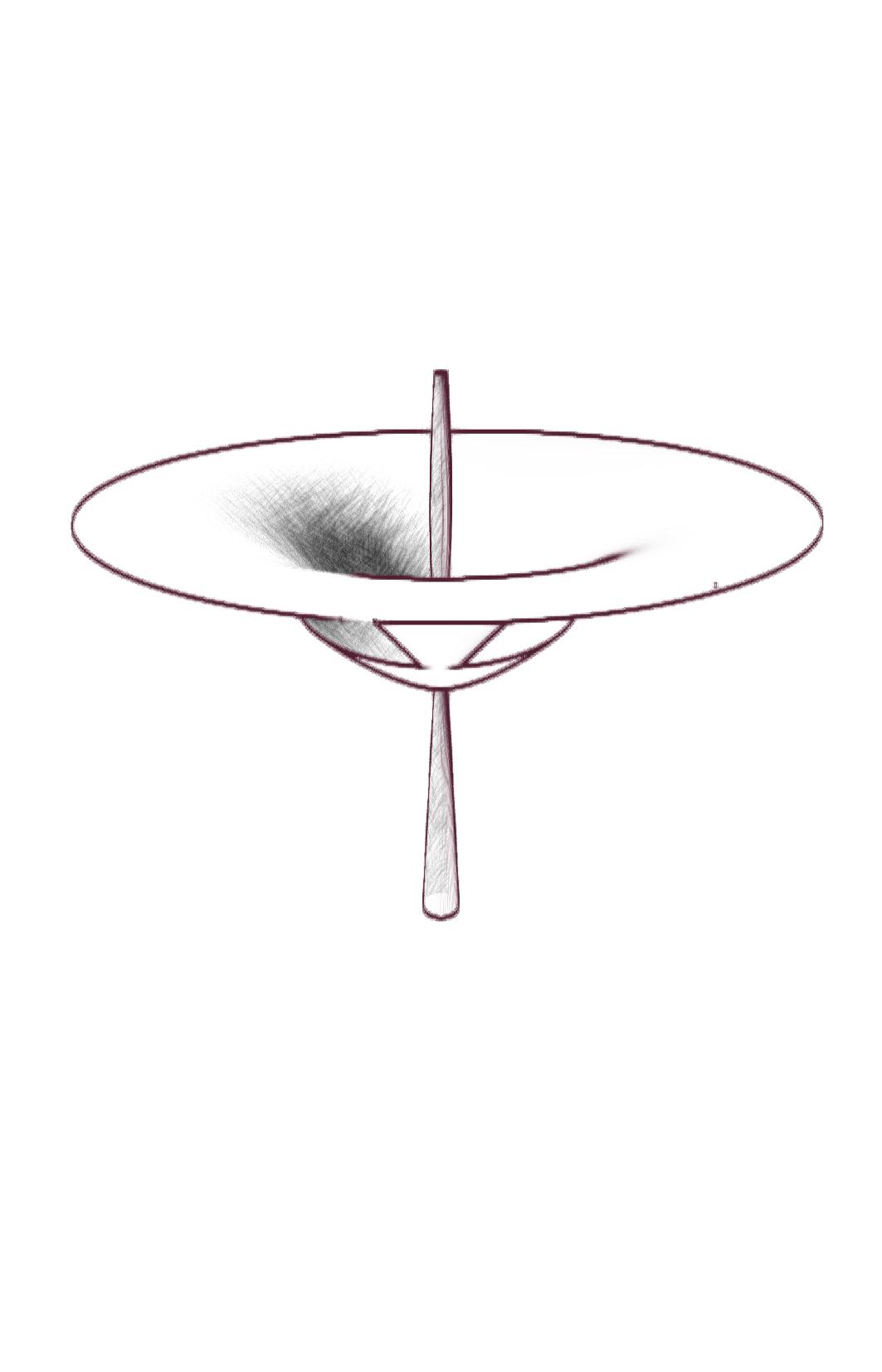
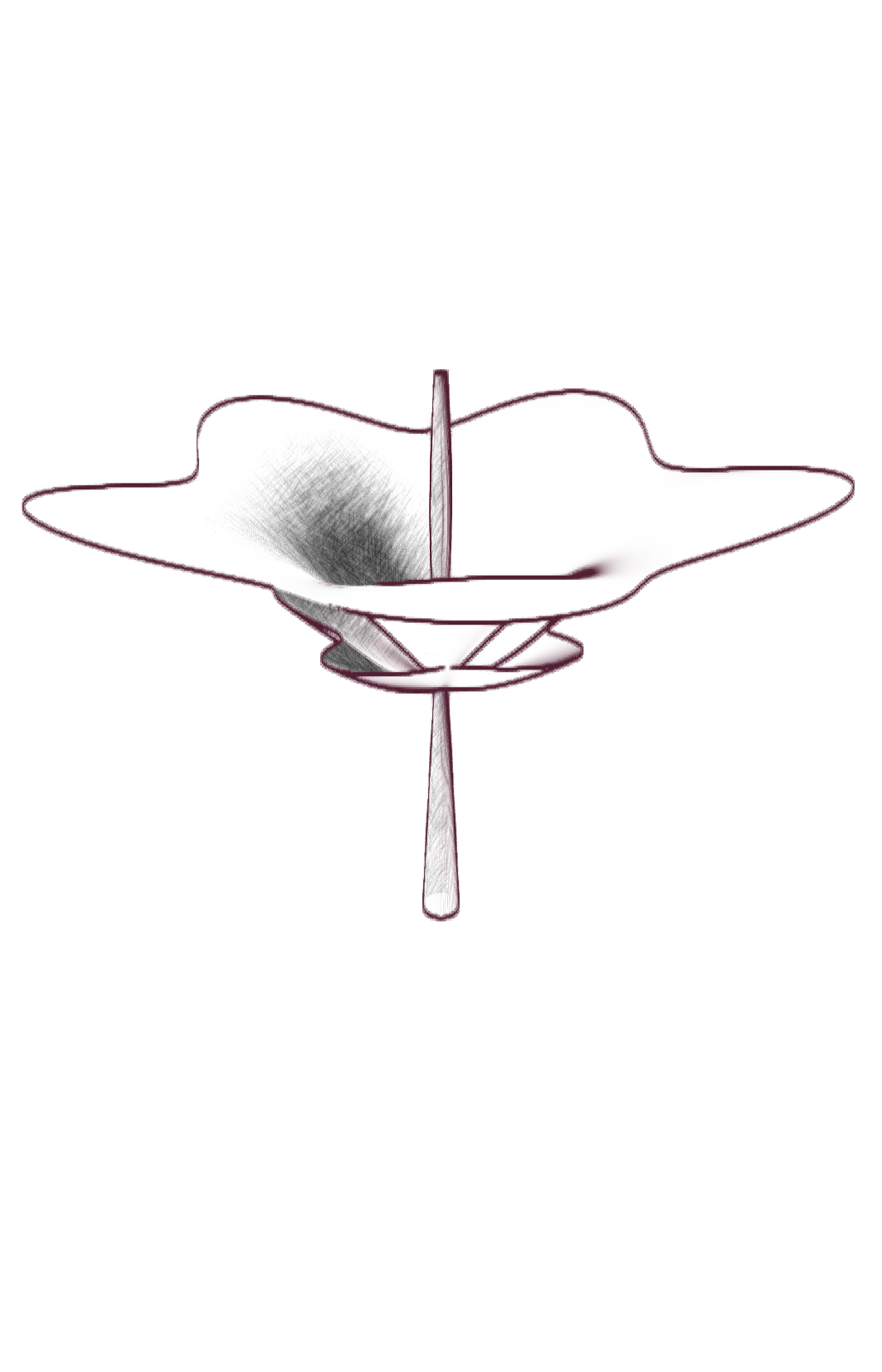
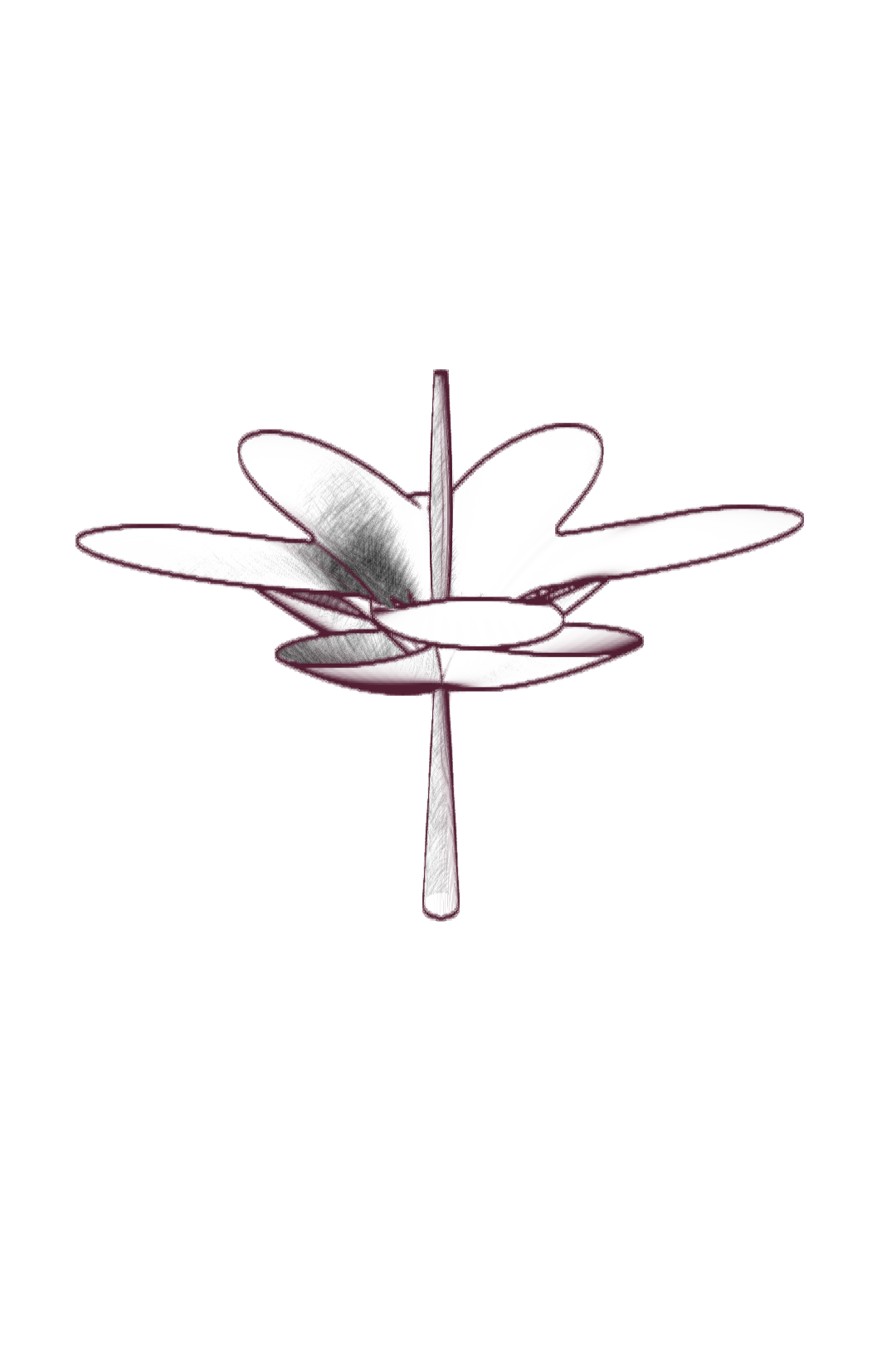
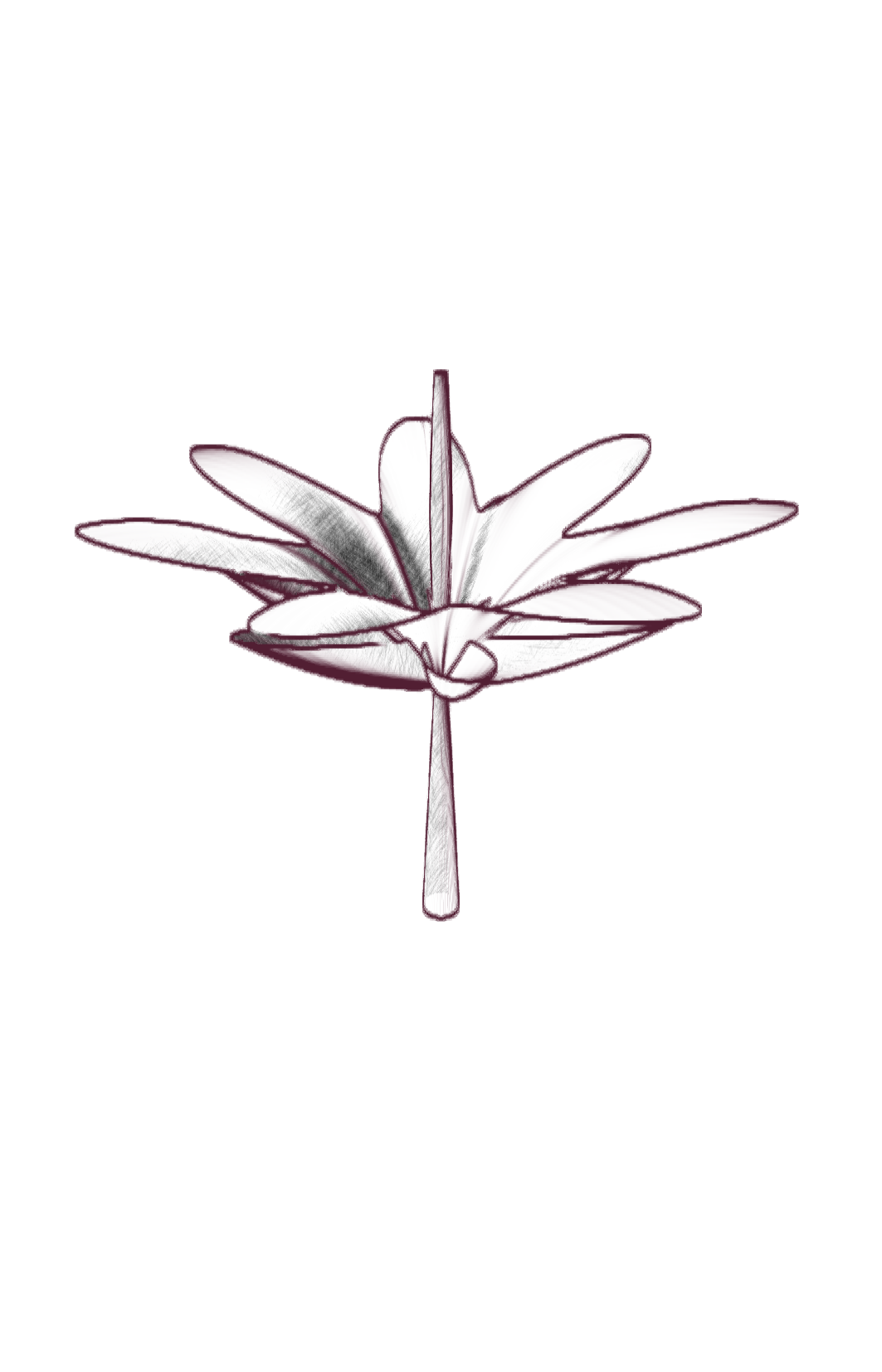
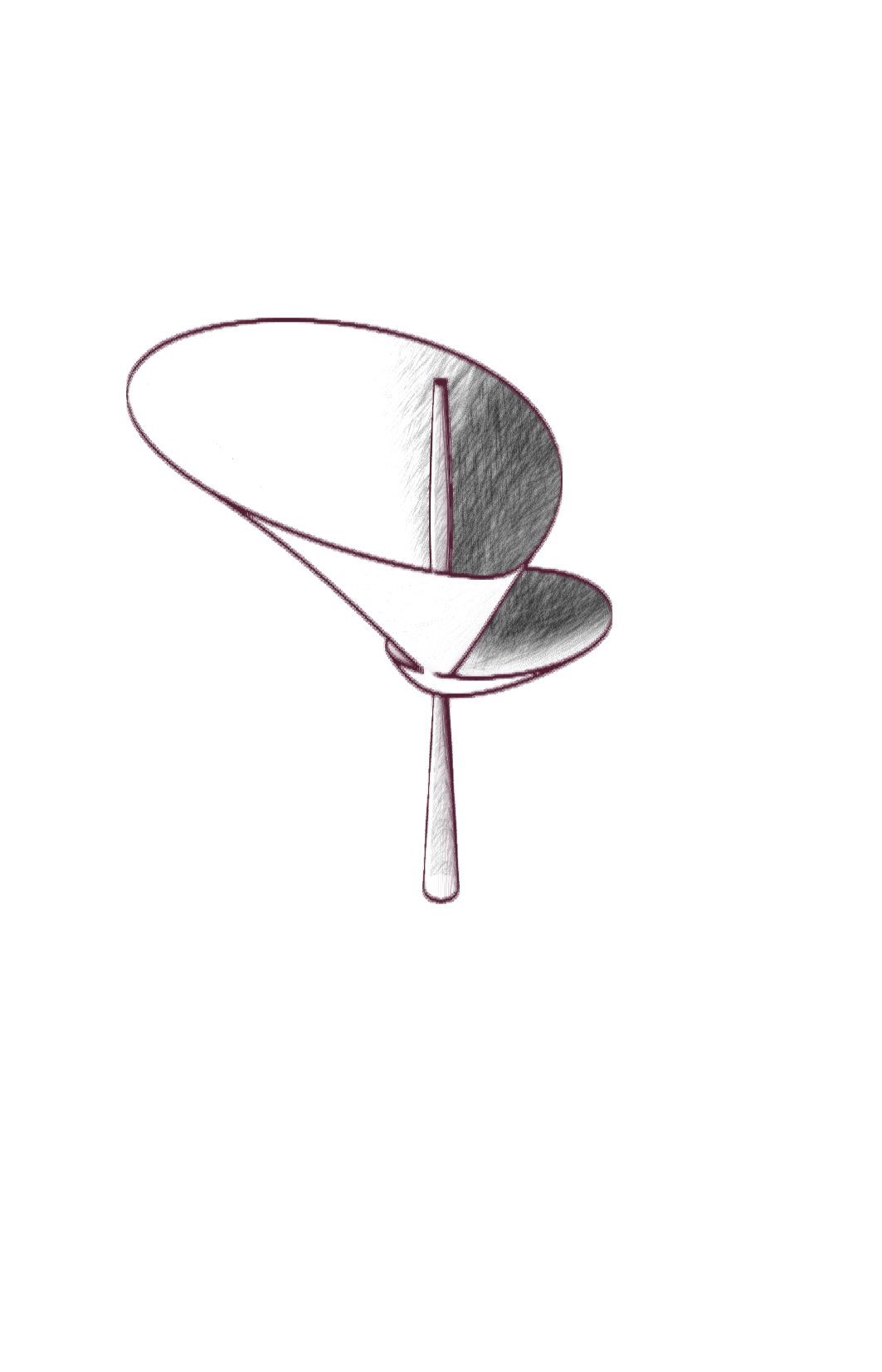
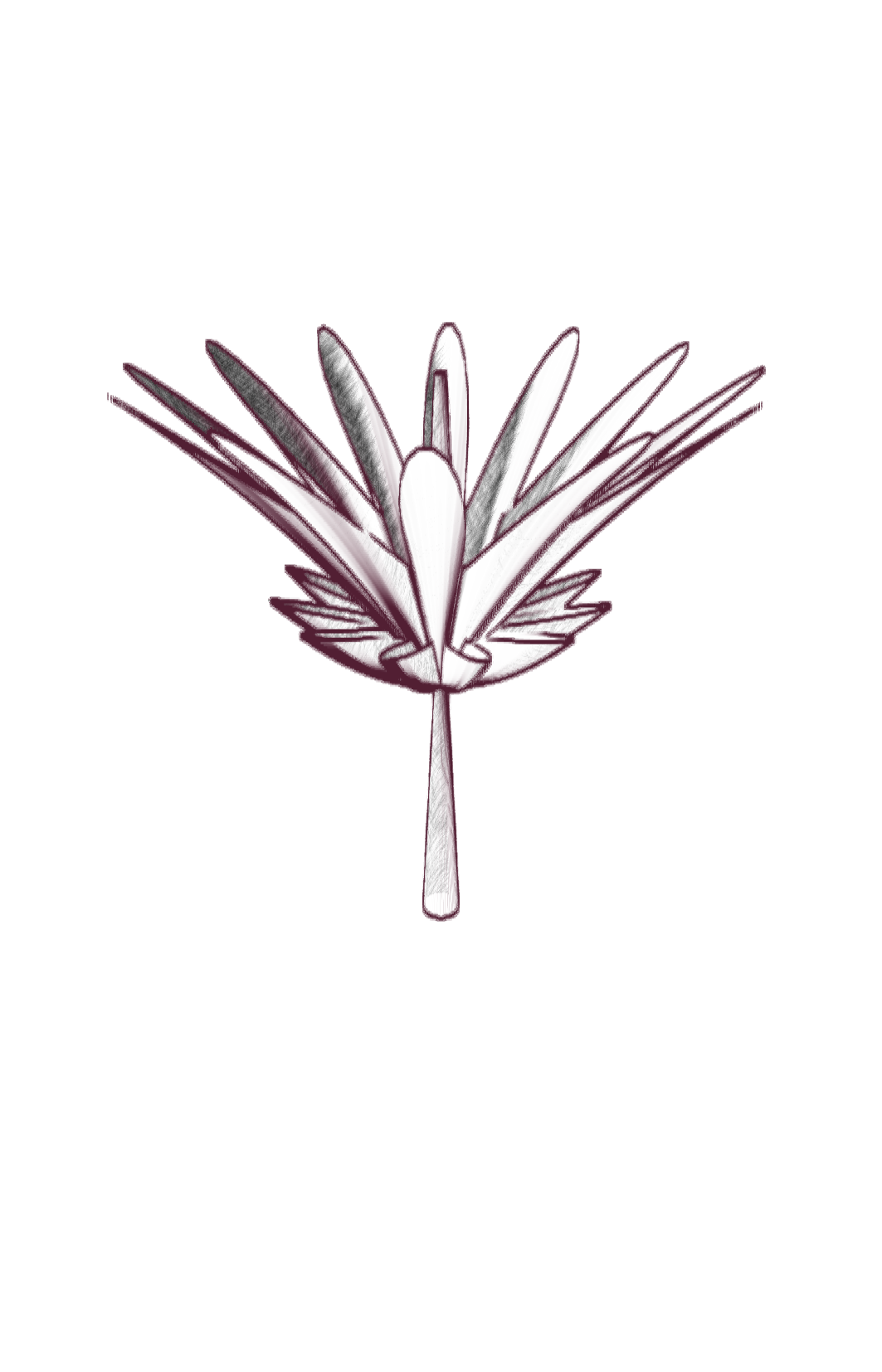
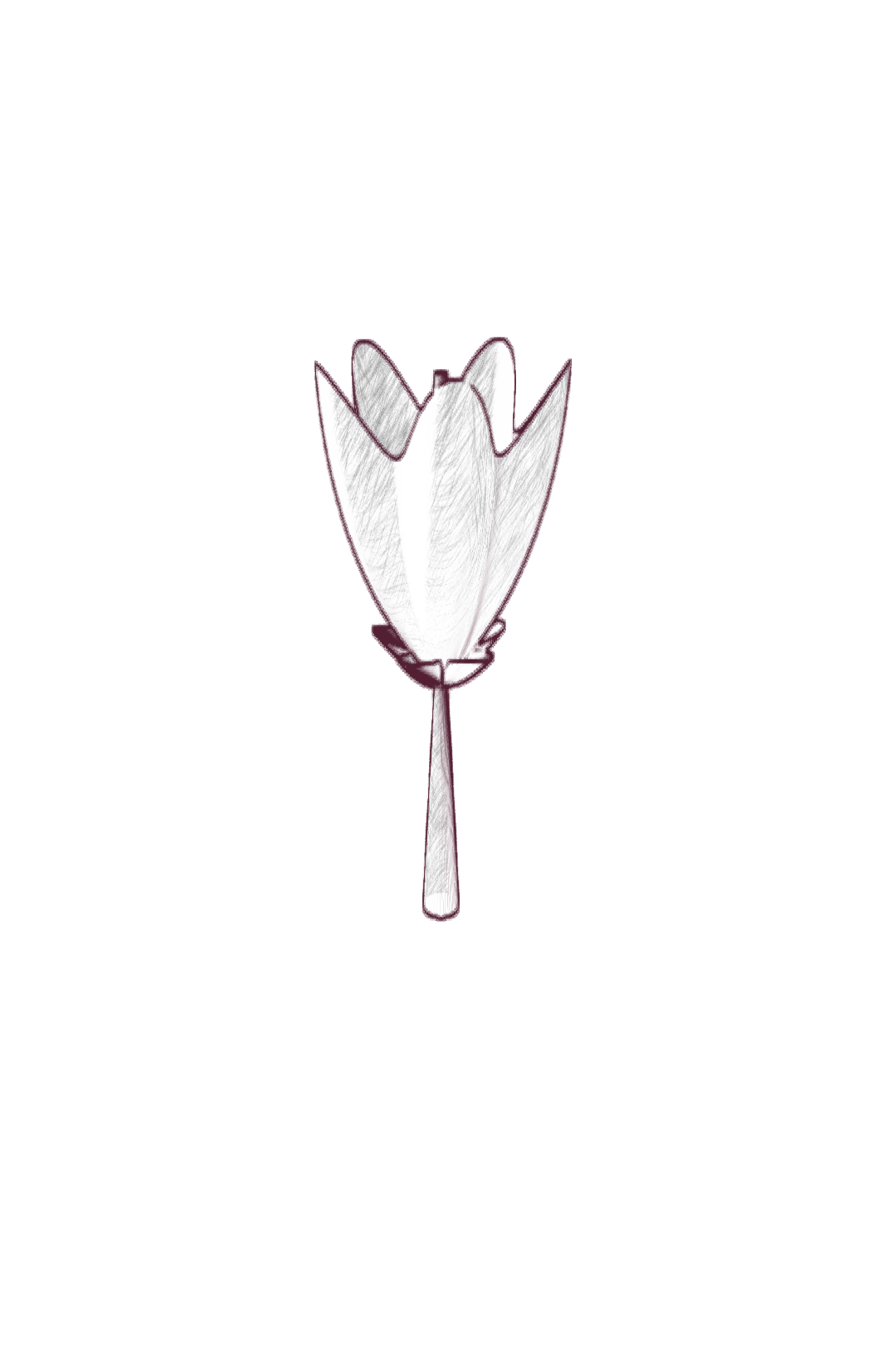
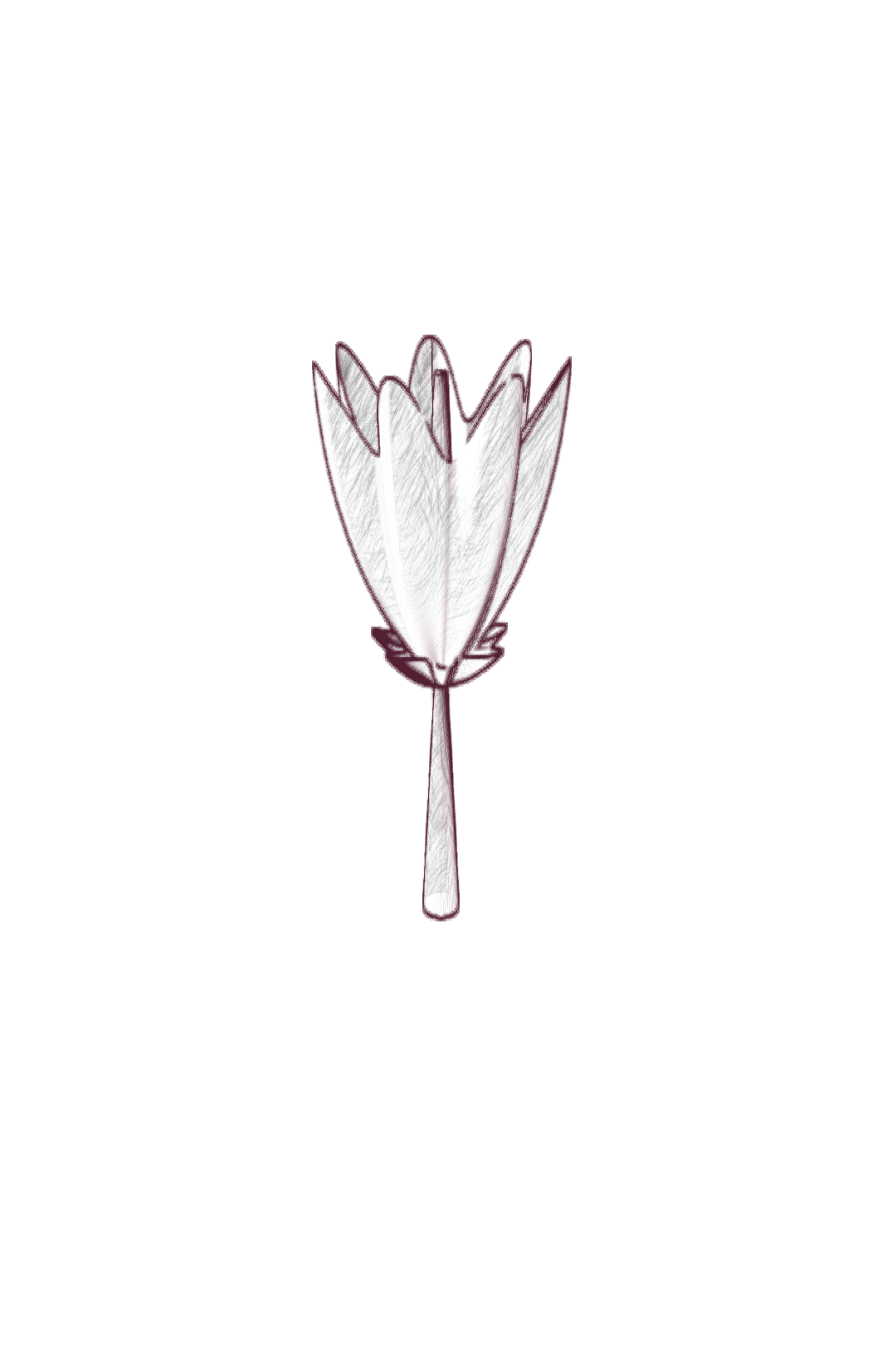
Ce projet est un hommage à Laurent Nottale, physicien théoricien français, qui a développé la théorie de la relativité d’échelle. Nous proposons ici de visualiser la diversité de ces formes issues des fonctions paramétriques, relativement simples, proposées par Laurent Nottale pour illustrer la morphogenèse de certaines fleurs.
Cette théorie propose une vision fractale de l’univers, où les lois de la physique sont invariantes par changement d’échelle. Cette vision est illustrée par des fractales (au sens étendu), des objets mathématiques régis par des lois d’échelle. L’espace-temps est fondamentalement fractal, traversée par d’infinies géodésiques, et on peut en dériver l’équation de Schrödinger, qui décrit l’évolution des fonctions d’onde en mécanique quantique à l’échelle microscopique. Certains phénomènes de croissance, comme ceux qui partent d’un centre, reflètent également cette structure fractale fondamentale et peuvent s’écrire sous forme de « potentiel quantique » : la diffusion des électrons dans un atome, la formation des nébuleuses planétaires, la morphogenèse des fleurs, etc. Il suffit d’un potentiel central et d’une symétrie sphérique, et les solutions de l’équation sont des discrétisations du moment angulaire, qui se traduisent par des formes géométriques :
[…] Une morphologie plus probable est obtenue en « envoyant » de la matière le long d’angles de probabilité maximale. Les contraintes biologiques conduisent à passer à la symétrie cylindrique. Cela conduit dans le cas le plus simple à une quantification périodique de l’angle θ (mesuré par un nombre quantique supplémentaire k), qui donne lieu à une séparation de “pétales” discrétisés. En outre, il existe une rupture de symétrie discrète le long de l’axe z liée à l’orientation (séparation du « haut » et du « bas » due à la gravité, croissance à partir d’une tige). Les solutions ainsi obtenues présentent des formes florales de type « tulipe » […].1
Le titre est repris de l’ouvrage issu de la collaboration entre Jean Chaline, Laurent Nottale, et Pierre Grou.2
Installation en local
Prérequis
Installation
git clone
cd fleurs-schrodinger
yarn installLancer le serveur de développement
yarn devBuild
yarn build